
Trong phân tích dữ liệu, việc kiểm tra tính chất phân phối của biến là rất quan trọng. Hai chỉ số thường được sử dụng để đánh giá phân phối của dữ liệu là Skewness (độ lệch) và Kurtosis (độ nhọn). Các chỉ số này giúp xác định liệu dữ liệu có tuân theo phân phối chuẩn hay không, từ đó quyết định phương pháp phân tích phù hợp.
1. Chỉ số Độ lệch (Skewness)
a. Định nghĩa Skewness
Chỉ số Skewness (độ lệch) là một tham số thống kê dùng để mô tả mức độ bất đối xứng của phân phối dữ liệu so với trung bình. Nói cách khác, Skewness cho biết phân phối có xu hướng nghiêng về bên trái hay bên phải so với giá trị trung tâm.
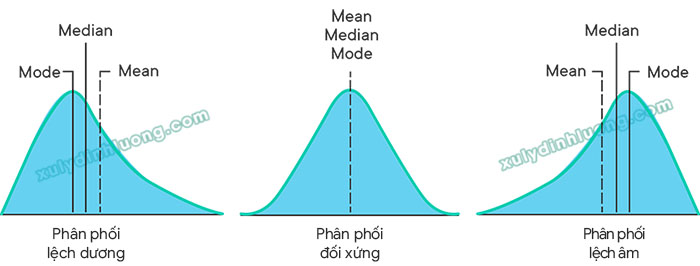
Phân phối dữ liệu có thể có ba hình thái điển hình như sau:
-
Skewness > 0 (Trung bình > Trung vị):
→ Phân phối lệch dương (positive skewness) hay lệch phải. Đặc trưng bởi phần đuôi bên phải kéo dài hơn bên trái. Phân phối này thường không tuân theo chuẩn. -
Skewness = 0 (Trung bình = Trung vị = Mode):
→ Phân phối đối xứng (symmetrical distribution). Đường phân phối có hai bên cân đối, là đặc điểm lý tưởng của phân phối chuẩn. -
Skewness < 0 (Trung bình < Trung vị):
→ Phân phối lệch âm (negative skewness) hay lệch trái. Đặc trưng bởi phần đuôi bên trái kéo dài hơn bên phải. Thường không đảm bảo phân phối chuẩn.
b. Đánh giá phân phối chuẩn thông qua chỉ số Skewness
Chỉ số Skewness phản ánh mức độ đối xứng của phân phối dữ liệu. Nếu phân phối kéo dài về phía một bên (trái hoặc phải), tức là phân phối bị lệch.
-
Phân phối lệch âm: Đuôi kéo dài về bên trái, thể hiện phần lớn giá trị lớn hơn trung bình.
-
Phân phối lệch dương: Đuôi kéo dài về bên phải, thể hiện phần lớn giá trị nhỏ hơn trung bình.
Theo Hair và cộng sự (2022), mức độ lệch có thể được sử dụng để đánh giá mức độ tiệm cận phân phối chuẩn như sau:
- Skewness từ -1 đến +1: Được xem là lý tưởng, có thể kết luận dữ liệu có phân phối chuẩn.
- Skewness từ -2 đến +2: Mức chấp nhận được, dữ liệu vẫn có thể được xem là phân phối chuẩn.
- Skewness < -2 hoặc > +2: Độ lệch quá lớn, dữ liệu được xem là không có phân phối chuẩn.
2. Chỉ số độ nhọn (Kurtosis)
a. Định nghĩa Kurtosis
Kurtosis là một chỉ số thống kê dùng để mô tả hình dạng phân phối dữ liệu, cụ thể là độ “nhọn” của đỉnh và độ “dày” của phần đáy trong phân phối.
- Nếu Kurtosis cao, điều này cho thấy phân phối có xu hướng tập trung nhiều giá trị ở phần đáy, tạo nên một đỉnh nhọn và hẹp.
- Nếu Kurtosis thấp, dữ liệu có xu hướng tập trung quanh đỉnh, dẫn đến một đỉnh rộng và thấp.
Theo công thức gốc, phân phối chuẩn có Kurtosis = 3. Tuy nhiên, để đơn giản hóa việc diễn giải, nhiều tài liệu, giáo trình và phần mềm thống kê (bao gồm SPSS) đã điều chỉnh giá trị này về 0, gọi là Excess Kurtosis (độ nhọn dư thừa), theo công thức: Excess Kurtosis = Kurtosis − 3.
Trong SPSS, mặc dù chỉ số được hiển thị dưới tên “Kurtosis”, nhưng thực chất đó là Excess Kurtosis. Vì vậy, khi phân tích kết quả, ta cần so sánh với giá trị 0, không phải 3.
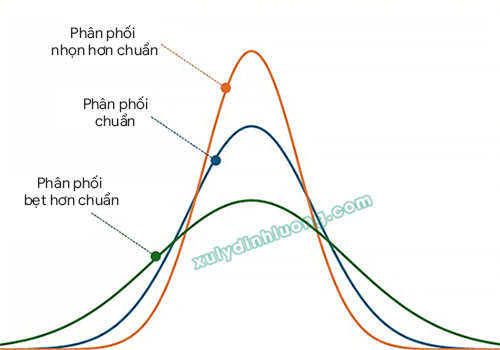
Các dạng hình thái phân phối theo chỉ số Excess Kurtosis:
-
Excess Kurtosis > 0:
→ Phân phối nhọn hơn chuẩn (Leptokurtic). Đỉnh đồ thị cao và sắc nét. -
Excess Kurtosis = 0:
→ Phân phối chuẩn (Mesokurtic). Đỉnh đồ thị có độ nhọn trung bình, tương ứng với phân phối chuẩn. -
Excess Kurtosis < 0:
→ Phân phối bẹt hơn chuẩn (Platykurtic). Đỉnh đồ thị thấp, rộng và ít nhọn.
b. Đánh giá phân phối chuẩn thông qua chỉ số Kurtosis
Chỉ số Kurtosis phản ánh mức độ “nhọn” hay “bẹt” của một phân phối so với phân phối chuẩn. Một giá trị Kurtosis dương cho thấy phân phối có đỉnh cao và sắc nhọn, trong khi giá trị âm phản ánh phân phối có đỉnh thấp và phẳng hơn.
Theo hướng dẫn của Hair và cộng sự (2022), khi sử dụng Kurtosis đã điều chỉnh (Excess Kurtosis – tức là Kurtosis đã trừ 3), có thể đánh giá mức độ chuẩn của phân phối như sau:
- Kurtosis ≈ 0: cho thấy phân phối gần như chuẩn – mức lý tưởng.
- Kurtosis trong khoảng từ -2 đến 2: phân phối được chấp nhận là gần chuẩn, không có sai lệch đáng kể.
- Kurtosis < -2 hoặc > 2: phân phối không tuân theo phân phối chuẩn.
3. Cách tính chỉ số Skewness và Kurtosis trong SPSS
Để tính hai chỉ số Skewness (độ lệch) và Kurtosis (độ nhọn) trong SPSS, bạn thực hiện tương tự như khi thống kê giá trị trung bình. Trên giao diện SPSS, vào menu Analyze → Descriptive Statistics → Descriptives.
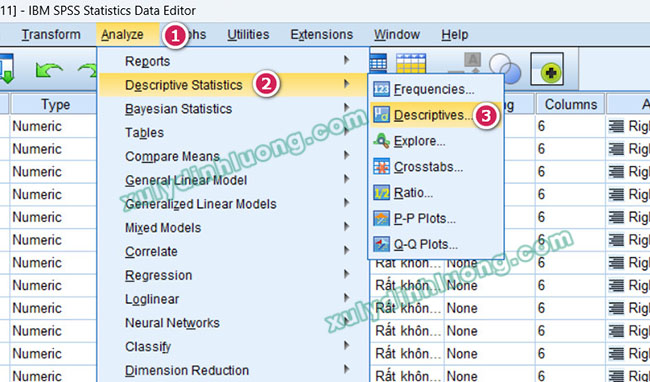
Trong cửa sổ Descriptives, đưa các biến định lượng cần kiểm tra vào ô Variable(s).

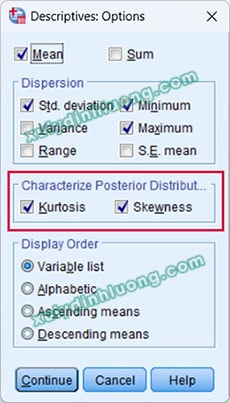
Nhấp vào nút Options…, sau đó đánh dấu chọn vào hai mục Skewness và Kurtosis.. Sau đó nhấp Continue quay về cửa sổ ban đầu rồi chọn OK để xuất kết quả ra output.
Kết quả được hiển thị trong bảng Descriptive Statistics, trong đó bao gồm giá trị Skewness và Kurtosis cho từng biến.
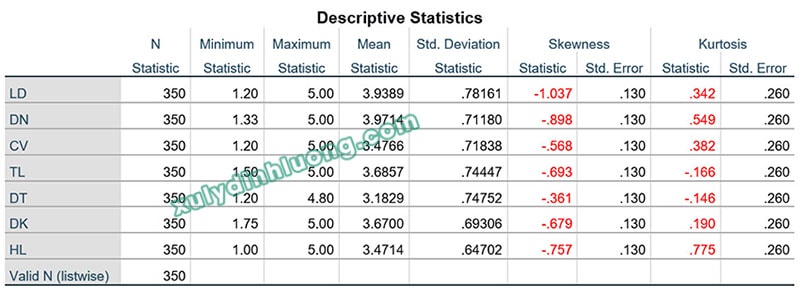
→ Giá trị Skewness và Kurtosis của các biến đều nằm trong khoảng từ -2 đến 2, như vậy, dữ liệu các biến này đều có phân phối xấp xỉ chuẩn.
Lưu ý:
Việc đánh giá phân phối chuẩn nên kết hợp cùng lúc nhiều phương thức đánh giá: dựa vào giá trị Skewness và Kurtosis, đồ thị P-P Plot, đồ thị Q-Q Plot, biểu đồ Histogram, kiểm định Shapiro-Wilk và Kolmogorov-Smirnov … để có kết luận chính xác nhất.
Xem thêm: Kiểm định Shapiro-Wilk và Kolmogorov-Smirnov trong SPSS
———-
Nguồn tham khảo:
Hair và cộng sự (2022). A Primer on Partial Least Squares Structural Equation Modeling (PLS-SEM) (3 ed.). Thousand Oaks, CA: Sage.





