
Phân phối chuẩn (Normal Distribution) là một giả định then chốt trong nhiều phương pháp kiểm định thống kê mang tính tham số. Nếu dữ liệu không tuân theo phân phối chuẩn, kết quả phân tích có thể bị sai lệch, dẫn đến những kết luận thiếu chính xác và không đáng tin cậy. Vì vậy, việc kiểm tra tính chuẩn của dữ liệu là bước khởi đầu quan trọng trước khi tiến hành các phân tích thống kê chuyên sâu.
Trong phần mềm SPSS, hai phương pháp kiểm định phổ biến nhất để đánh giá phân phối chuẩn là Shapiro-Wilk (kiểm định S-W) và Kolmogorov-Smirnov (kiểm định K-S). Bài viết này sẽ hướng dẫn chi tiết cách thực hiện hai kiểm định này trong SPSS, cách diễn giải kết quả, cũng như những điểm cần lưu ý khi áp dụng.
1. Cơ chế của kiểm định Shapiro–Wilk và Kolmogorov–Smirnov
Theo Andy Field (2009), một cách phổ biến để đánh giá liệu dữ liệu có tuân theo phân phối chuẩn hay không là so sánh phân phối thực tế của dữ liệu với một phân phối chuẩn lý tưởng có cùng giá trị trung bình và độ lệch chuẩn. Hai kiểm định thống kê thường được sử dụng cho mục đích này là Shapiro–Wilk và Kolmogorov–Smirnov.
Nói cách khác, chúng ta giả định có một phân phối chuẩn làm chuẩn đối chiếu (gọi là A), và so sánh với phân phối của tập dữ liệu thực tế (gọi là B). Cả hai phân phối được đặt trong cùng một hệ quy chiếu — tức là có cùng trung bình và độ lệch chuẩn — để đảm bảo tính khách quan khi so sánh. Nếu phân phối B gần khớp với A, dữ liệu có thể được xem là phân phối chuẩn. Ngược lại, nếu sự khác biệt giữa B và A đủ lớn, dữ liệu sẽ bị xem là không tuân theo phân phối chuẩn. Hai kiểm định Shapiro–Wilk và Kolmogorov–Smirnov chính là công cụ giúp đánh giá mức độ khác biệt này.
Cách diễn giải kết quả kiểm định:
-
Nếu giá trị sig (p-value) > 0.05: không có sự khác biệt có ý nghĩa thống kê giữa dữ liệu và phân phối chuẩn → có thể xem là dữ liệu tuân theo phân phối chuẩn.
-
Nếu giá trị sig < 0.05: có sự khác biệt có ý nghĩa thống kê giữa dữ liệu và phân phối chuẩn → dữ liệu không phân phối chuẩn.
Ở bề ngoài, hai kiểm định này dường như rất tiện lợi vì chỉ cần dựa vào một giá trị sig duy nhất là có thể đưa ra kết luận. Tuy nhiên, chúng cũng tồn tại những hạn chế nhất định. Đặc biệt, trong các tập dữ liệu có kích thước lớn, thậm chí một sai lệch rất nhỏ so với phân phối chuẩn cũng có thể dẫn đến giá trị sig < 0.05, khiến kiểm định báo hiệu dữ liệu không chuẩn, dù thực tế sai lệch đó có thể không đáng kể và không ảnh hưởng nhiều đến các phân tích tiếp theo.
Ví dụ minh họa:
Giả sử bạn có dữ liệu về độ tuổi của 500 người và muốn kiểm tra tính chuẩn. Khi chạy kiểm định Shapiro–Wilk, bạn thu được kết quả sig = 0.03 (< 0.05) → về mặt thống kê, đây là dấu hiệu cho thấy dữ liệu không tuân theo phân phối chuẩn. Tuy nhiên, nếu bạn kiểm tra thêm bằng biểu đồ Histogram hoặc Q-Q plot và thấy phân phối chỉ hơi lệch nhẹ, không có ngoại lệ nghiêm trọng, thì trong thực tế, bạn vẫn có thể sử dụng các kiểm định tham số vốn yêu cầu điều kiện phân phối chuẩn, mà không ảnh hưởng đến độ tin cậy của kết quả.
Lưu ý quan trọng từ Andy Field (2009):
Đối với các mẫu có kích thước lớn, cả hai kiểm định Shapiro–Wilk và Kolmogorov–Smirnov có xu hướng dễ phát hiện sự khác biệt có ý nghĩa thống kê, ngay cả khi dữ liệu chỉ lệch rất nhẹ so với phân phối chuẩn. Điều này có thể dẫn đến việc đánh giá sai lệch rằng dữ liệu không chuẩn, trong khi sai lệch đó không thật sự đáng kể về mặt thực tiễn.
Vì vậy, không nên chỉ dựa duy nhất vào kết quả kiểm định để kết luận về tính phân phối chuẩn của dữ liệu. Thay vào đó, nên kết hợp với các phương pháp bổ trợ trực quan và định lượng khác, bao gồm:
-
Biểu đồ Histogram
-
Biểu đồ P–P plot hoặc Q–Q plot
-
Giá trị độ lệch (Skewness)
-
Giá trị độ nhọn (Kurtosis)
Sự kết hợp này sẽ giúp đưa ra đánh giá toàn diện và đáng tin cậy hơn về đặc điểm phân phối của dữ liệu.
2. Cỡ mẫu phù hợp cho kiểm định Shapiro–Wilk và Kolmogorov–Smirnov
Theo đề xuất của Prabhakar Mishra và cộng sự (2019), việc lựa chọn kiểm định phù hợp để đánh giá phân phối chuẩn nên dựa trên cỡ mẫu cụ thể như sau:
-
Kiểm định Shapiro–Wilk được xem là lý tưởng nhất với cỡ mẫu nhỏ (≤ 50). Mặc dù vẫn có thể áp dụng cho các mẫu lớn hơn (lên đến khoảng 2000 tùy theo phần mềm), nhưng kiểm định này phát huy ưu thế rõ rệt khi dùng cho mẫu nhỏ, nhờ khả năng phát hiện sai lệch rất nhạy.
-
Kiểm định Kolmogorov–Smirnov thích hợp hơn với các mẫu có kích thước trung bình đến lớn (≥ 50). Trong trường hợp mẫu nhỏ hơn 50, kiểm định này có độ nhạy kém và có thể dẫn đến kết quả thiếu chính xác.
Tác giả cũng lưu ý rằng, mặc dù hai kiểm định này có cơ chế đánh giá tương tự nhau, Shapiro–Wilk thường nhạy hơn trong việc phát hiện sự khác biệt so với phân phối chuẩn. Do đó, trong một số trường hợp, bạn có thể thấy Shapiro–Wilk cho kết quả có ý nghĩa thống kê (sig < 0.05) trong khi Kolmogorov–Smirnov lại không, đặc biệt khi dữ liệu chỉ lệch nhẹ khỏi chuẩn.
Kết luận khuyến nghị sử dụng:
-
Với cỡ mẫu ≤ 50 → Ưu tiên sử dụng Shapiro–Wilk.
-
Với cỡ mẫu ≥ 50 → Có thể sử dụng cả hai, tuy nhiên Shapiro–Wilk vẫn được khuyến khích hơn nhờ độ nhạy cao hơn.
-
Luôn kết hợp với các phương pháp bổ trợ:
-
Biểu đồ Histogram, Q–Q plot
-
Chỉ số Skewness và Kurtosis
để đưa ra đánh giá toàn diện và đáng tin cậy hơn về tính phân phối chuẩn của dữ liệu.
-
Xem thêm: Dịch vụ xử lý SPSS uy tín
3. Kiểm định phân phối chuẩn bằng Shapiro-Wilk và Kolmogorov-Smirnov trong SPSS
3.1 Cách thực hiện Shapiro-Wilk và Kolmogorov-Smirnov trong SPSS
Ở đây, chúng ta có một tập dữ liệu thực hành với cỡ mẫu N = 200, gồm ba biến định lượng cần được đánh giá về tính phân phối chuẩn, bao gồm:
-
Biến HaiLong: Trung bình cộng của các biến quan sát đo lường mức độ hài lòng trên thang đo Likert từ 1 đến 5.
-
Biến DoTuoi: Tuổi của các đáp viên, dao động trong khoảng từ 19 đến 40 tuổi.
-
Biến ThuNhap: Thu nhập hàng tháng của đáp viên, đơn vị tính là triệu VNĐ.
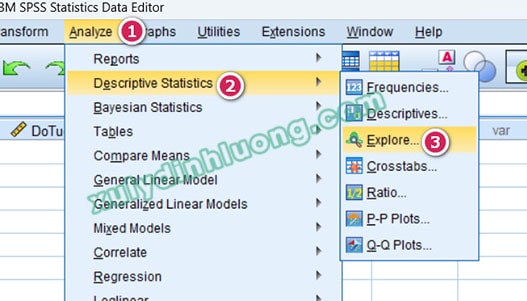
Để kiểm tra phân phối chuẩn bằng hai kiểm định Shapiro-Wilk và Kolmogorov-Smirnov, chúng ta vào Analyze > Descriptive Statistics > Explore…
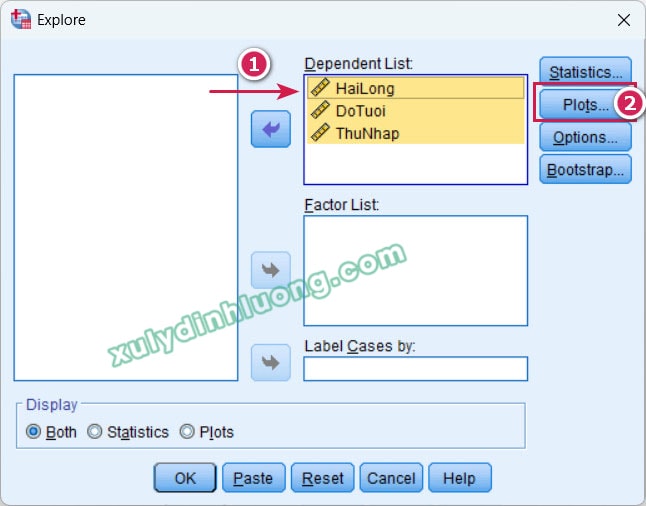
Tại hộp thoại Explore, chọn các biến cần kiểm định và đưa vào ô Dependent List (bằng cách kéo-thả hoặc dùng nút mũi tên). Nếu muốn thực hiện kiểm định riêng theo từng nhóm (ví dụ: nam và nữ), hãy đưa biến phân nhóm vào ô Factor List. Nhấn nút “Plots…” ở bên phải hộp thoại.
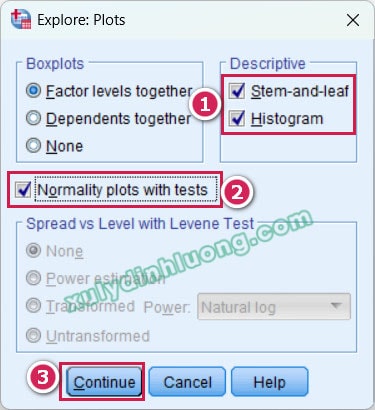
Trong hộp thoại Plots, tích chọn các mục: Stem-and-leaf, Histogram. Quan trọng nhất, hãy tích chọn “Normality plots with tests” — đây là tùy chọn bắt buộc để SPSS thực hiện và hiển thị kết quả của hai kiểm định Shapiro–Wilk và Kolmogorov–Smirnov. Nhấn Continue để quay lại hộp thoại chính.
Tại hộp thoại Explore, nhấn OK để chạy phân tích và xuất kết quả ra cửa sổ Output.
Sau khi hoàn tất, SPSS sẽ hiển thị nhiều bảng và biểu đồ phục vụ việc đánh giá tính chuẩn. Tuy nhiên, trong phạm vi bài viết này, chúng ta sẽ tập trung vào bảng “Tests of Normality” – nơi thể hiện rõ kết quả hai kiểm định Shapiro–Wilk và Kolmogorov–Smirnov cho từng biến.
3.2 Đọc kết quả kiểm định Shapiro-Wilk và Kolmogorov-Smirnov trong SPSS
Trong bảng Tests of Normality, chúng ta sẽ thấy hai phần chính là kết quả kiểm định Kolmogorov-Smirnov và Shapiro-Wilk với các thông số
- Statistic: Giá trị thống kê của kiểm định.
- df (Degrees of Freedom): Bậc tự do.
- Sig. (Asymp. Sig. (2-tailed)): Giá trị sig (mức ý nghĩa).
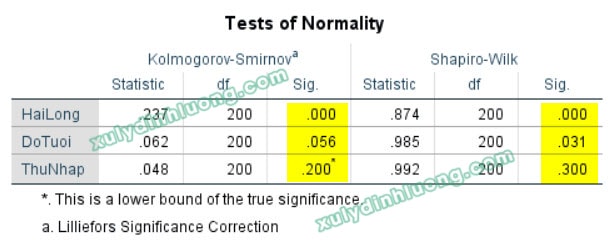
Cỡ mẫu của dữ liệu này là 200 (lớn hơn 50), nên chúng ta có thể sử dụng cả hai kiểm định Kolmogorov-Smirnov và Shapiro-Wilk để đánh giá kết quả.
Biến “HaiLong”
- Kolmogorov-Smirnov: Sig. = 0.000 < 0.05
- Shapiro-Wilk: Sig. = 0.000 < 0.05
→ Kết luận: Cả hai kiểm định đều cho giá trị Sig. = 0.000, nhỏ hơn 0.05. Điều này có nghĩa là biến HaiLong không có phân phối chuẩn.
Biến “DoTuoi”
- Kolmogorov-Smirnov: Sig. = 0.056 > 0.05
- Shapiro-Wilk: Sig. = 0.031 < 0.05
→ Kết luận: Kolmogorov-Smirnov (Sig. = 0.056 > 0.05) cho thấy có thể chấp nhận giả thuyết phân phối chuẩn. Shapiro-Wilk (Sig. = 0.031 ≤ 0.05) lại cho thấy bác bỏ giả thuyết phân phối chuẩn.
Trong trường hợp này, kết quả hai kiểm định cho thấy có một mức độ mâu thuẫn nhẹ. Với cỡ mẫu lớn (N = 200), kiểm định Kolmogorov–Smirnov thường được ưu tiên sử dụng hơn do phù hợp với mẫu trung bình đến lớn. Tuy nhiên, khi xuất hiện sự không nhất quán giữa hai kiểm định — và đặc biệt khi giá trị sig của Kolmogorov–Smirnov chỉ nhỉnh hơn 0.05 một chút — chúng ta không nên vội vàng đưa ra kết luận. Thay vào đó, cần kết hợp đánh giá thêm bằng các công cụ trực quan và thống kê bổ trợ, bao gồm:
- Biểu đồ Histogram với đường cong phân phối chuẩn,
- Biểu đồ Q–Q plot và P–P plot,
- Các chỉ số Skewness (độ lệch) và Kurtosis (độ nhọn).
Nếu các biểu đồ và chỉ số định lượng này tiệm cận với đặc điểm của phân phối chuẩn, bạn có thể cân nhắc rằng biến DoTuoi phân phối tương đối chuẩn, hoặc ít nhất không có sai lệch đáng kể so với phân phối chuẩn.
Tuy nhiên, cần lưu ý rằng kiểm định Shapiro–Wilk đã cho kết quả có ý nghĩa thống kê (sig < 0.05), tức là cảnh báo dữ liệu không phân phối chuẩn — và đây được xem là một tín hiệu khá mạnh do Shapiro–Wilk có độ nhạy cao hơn. Trong thực hành, nếu một trong hai kiểm định cho thấy vi phạm tính chuẩn, đặc biệt khi giá trị sig của Kolmogorov–Smirnov cũng tiệm cận ngưỡng 0.05, thì chúng ta nên thận trọng và nghiêng về kết luận rằng dữ liệu không hoàn toàn tuân theo phân phối chuẩn
Biến “ThuNhap”
- Kolmogorov-Smirnov: Sig. = 0.200 > 0.05
- Shapiro-Wilk: Sig. = 0.300 > 0.05
→ Kết luận: Cả hai kiểm định đều cho giá trị sig lớn hơn 0.05 (0.200 và 0.300). Điều này có nghĩa là biến ThuNhap có phân phối chuẩn.
KẾT LUẬN:
HaiLong: Không có phân phối chuẩn.
DoTuoi: Có khả năng không có phân phối chuẩn, cần kiểm tra thêm trực quan (biểu đồ) và chỉ số Skewness/Kurtosis để khẳng định chắc chắn.
ThuNhap: Có phân phối chuẩn.
Xem thêm: Chỉ số Skewness và Kurtosis đánh giá phân phối chuẩn trong SPSS
———-
Nguồn tham khảo:
Shapiro, S. S., & Wilk, M. B. (1965). An analysis of variance test for normality (complete samples). Biometrika, 52(3/4), 591–611.
Mishra P, Pandey CM, Singh U, Gupta A, Sahu C, Keshri A. Descriptive statistics and normality tests for statistical data. Ann Card Anaesth. 2019 Jan-Mar;22(1):67-72.
Field, A. (2009) Discovering Statistics Using SPSS. 3rd Edition, Sage Publications Ltd., London.





