Phân tích tương quan, hồi quy khi mô hình có biến trung gian

Đối với mô hình có biến trung gian, số lượng hồi quy cần chạy sẽ tương ứng số lượng biến có vai trò phụ thuộc trong mô hình.

Xét mô hình nghiên cứu sau đây:

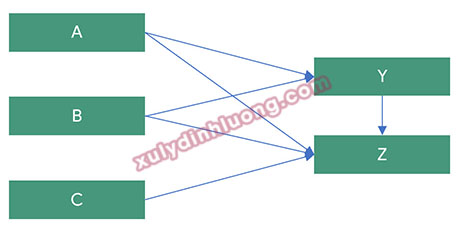
Chúng ta sẽ phân tích các vai trò biến của mô hình này:

– Biến A, B, C: đây là các biến chỉ có mũi tên đi ra, điều này nói lên rằng các biến này chỉ tác động lên biến khác chứ không nhận tác động về. Loại biến chỉ có mũi tên đi ra là các biến có vai trò độc lập hoàn toàn.

– Biến Z: đây là biến chỉ có mũi tên đi vào, điều này nói lên rằng biến này chỉ nhận tác động từ biến khác chứ không tác động lên biến khác. Loại biến chỉ có mũi tên hướng vào là các biến có vai trò phụ thuộc hoàn toàn.

– Biến Y: đây là biến vừa có mũi tên đi vào vừa có mũi tên đi ra, điều này nói lên rằng biến này vừa nhận tác động từ biến khác vào, vừa tác động lên biến khác. Loại biến vừa có mũi tên vào vừa có mũi tên ra là biến vừa có vai trò độc lập vừa có vai trò phụ thuộc.

Trong một mô hình, nếu có biến nào nhận mũi tên hướng vào thì biến đó có vai trò phụ thuộc. Biến trung gian là một biến có vai trò phụ thuộc. Trong ví dụ mô hình bên trên, biến Y và biến Z là hai biến có vai trò phụ thuộc.

1. Hồi quy mô hình có biến trung gian

Như vậy trong mô hình này, tổng cộng có hai biến nhận mũi tên hướng vào là Y và Z. Y, Z là hai biến có vai trò phụ thuộc. Để đánh giá tất cả các mối tác động trong mô hình, chúng ta sẽ triển khai hai hồi quy tương ứng hai biến có vai trò phụ thuộc. Mô hình có bao nhiêu biến có vai trò phụ thuộc sẽ phân tích bấy nhiêu hồi quy.

• Hồi quy 1: Y là phụ thuộc – A, B là độc lập.
• Hồi quy 2: Z là phụ thuộc – A, B, C, Y là độc lập.

Nếu kết quả hồi quy 2 xuất hiện sự cộng tuyến/ đa cộng tuyến dữ liệu của biến Y với biến A hoặc B hoặc cả hai biến do Y là phụ thuộc của A, B trong phép hồi quy 1, thì chúng ta sẽ thực hiện ba hồi quy cho mô hình này:

• Hồi quy 1: Y là phụ thuộc – A, B là độc lập.
• Hồi quy 2: Z là phụ thuộc – A, B, C là độc lập.
• Hồi quy 3: Z là phụ thuộc – Y là độc lập.

2. Tương quan mô hình có biến trung gian

Tương quan là kiểm định xét độc lập từng cặp biến với nhau, dù có hay không có mặt biến khác. Nghĩa là, khi bạn phân tích tương quan giữa A, B với nhau, hệ số tương quan giữa A-B là 0.6 thì khi phân tích tương quan A, B, C với nhau thì hệ số tương quan giữa A-B vẫn là 0.6.

Do phân tích bao nhiêu biến với nhau đi nữa thì kết quả tương quan của cặp biến đó cũng không thay đổi, nên bạn có thể đưa tất cả các biến trong mô hình vào phân tích tương quan cùng một lần và đánh giá tương quan từng cặp biến với nhau.

Thường chúng ta kỳ vọng:

• Biến độc lập và biến phụ thuộc trong một hồi quy sẽ có sig tương quan nhỏ hơn 0.05.
• Giữ các biến độc lập với nhau trong một hồi quy sẽ sig tương quan nhỏ hay lớn hơn 0.05 đều được nhưng hệ số tương quan nên nhỏ hơn 0.7 để tránh hiện tượng cộng tuyến dữ liệu (xem thêm ở bài viết Phân tích tương quan Pearson trong SPSS).

Cụ thể trong mô hình ví dụ ở trên, chúng ta sẽ đọc kết quả tương quan theo từng hồi quy. Giả sử mô hình này chúng ta triển khai hai hồi quy là:

• Hồi quy 1: Y là phụ thuộc – A, B là độc lập.
• Hồi quy 2: Z là phụ thuộc – A, B, C, Y là độc lập.