Phân tích nhân tố khám phá EFA trong SPSS

Phân tích nhân tố khám phá (Exploratory Factor Analysis – EFA) trong SPSS là một kỹ thuật thống kê mạnh mẽ được sử dụng để khám phá cấu trúc tiềm ẩn của một tập hợp lớn các biến quan sát. Mục tiêu chính của EFA là:

(1) Rút gọn dữ liệu: Giảm số lượng lớn các biến quan sát thành một tập hợp nhỏ hơn các “nhân tố” (factors) hoặc các khái niệm tiềm ẩn có ý nghĩa hơn.

(2) Xác định cấu trúc thang đo: Giúp nhận diện các biến quan sát nào thuộc về cùng một nhân tố, từ đó xây dựng hoặc kiểm định các thang đo.

(3) Khám phá mối quan hệ: Hiểu rõ hơn về các mối quan hệ tương quan giữa các biến quan sát và các nhân tố tiềm ẩn.

1. Ý nghĩa của phân tích nhân tố khám phá EFA

1. Rút gọn dữ liệu (Data Reduction)

Đây là ý nghĩa nổi bật nhất của EFA. Khi bạn có hàng chục, thậm chí hàng trăm biến quan sát (tương ứng với các câu hỏi khảo sát), việc phân tích từng biến riêng lẻ sẽ rất cồng kềnh và dễ dẫn đến sai sót. EFA giúp nhóm các biến có mối tương quan chặt chẽ lại với nhau thành các nhân tố tiềm ẩn. Điều này cho phép chúng ta làm việc với một số lượng nhân tố nhỏ hơn nhiều so với số lượng biến ban đầu, từ đó đơn giản hóa cấu trúc dữ liệu mà vẫn giữ được phần lớn thông tin quan trọng.

2. Khám phá cấu trúc tiềm ẩn của thang đo

Trong nghiên cứu, đặc biệt là trong các lĩnh vực khoa học xã hội, chúng ta thường đo lường các khái niệm trừu tượng (ví dụ: sự hài lòng của khách hàng, chất lượng dịch vụ, động lực làm việc) bằng nhiều câu hỏi hoặc biến quan sát khác nhau. EFA giúp khám phá xem những biến quan sát nào “thuộc” về cùng một khái niệm tiềm ẩn. Nó giúp xác định cấu trúc nội tại của thang đo, tức là các nhóm câu hỏi liên kết với nhau để đo lường một khía cạnh cụ thể của khái niệm lớn.

3. Nâng cao tính khái quát và ý nghĩa của nghiên cứu

Các nhân tố được trích xuất từ EFA thường đại diện cho các khái niệm hoặc khía cạnh rộng hơn mà các biến quan sát đang cố gắng đo lường. Điều này giúp nâng cao tính khái quát của các phát hiện, cho phép bạn đưa ra các kết luận ở cấp độ khái niệm thay vì chỉ ở cấp độ biến cụ thể. Ví dụ, thay vì nói “khách hàng thích thái độ phục vụ của nhân viên” và “khách hàng hài lòng với tốc độ phản hồi”, EFA có thể giúp tổng hợp lại thành một nhân tố chung là “Chất lượng dịch vụ hỗ trợ khách hàng”, mang ý nghĩa tổng quát hơn.

2. Tiêu chuẩn phân tích nhân tố EFA

2.1 Hệ số KMO (Kaiser-Meyer-Olkin)

Chỉ số KMO (Kaiser-Meyer-Olkin) được sử dụng để đánh giá mức độ phù hợp của dữ liệu cho phân tích nhân tố, thông qua việc so sánh giữa hệ số tương quan đơn giản và hệ số tương quan từng phần giữa các biến. Do tính chất phức tạp về mặt kỹ thuật, tài liệu này sẽ không đi sâu vào định nghĩa hay công thức tính toán cụ thể của chỉ số KMO.

Theo Kaiser (1974), giá trị KMO nên đạt từ 0.5 trở lên (0.5 ≤ KMO ≤ 1.0) để dữ liệu được xem là phù hợp cho phân tích nhân tố. Nếu chỉ số KMO thấp hơn 0.5, nhà nghiên cứu cần cân nhắc thu thập thêm dữ liệu, loại bỏ các biến quan sát không phù hợp, hoặc điều chỉnh lại thang đo.

Cũng cần lưu ý rằng, hệ số KMO chỉ là một trong những tiêu chí để đánh giá sự phù hợp của phân tích nhân tố. Để có cái nhìn toàn diện hơn, bạn cũng cần xem xét các yếu tố quan trọng khác như:

• Kích thước mẫu: Đảm bảo mẫu đủ lớn để có thể thực hiện phân tích nhân tố một cách đáng tin cậy.
• Độ tin cậy của dữ liệu: Kiểm tra tính nhất quán và ổn định của các biến quan sát.
• Ý nghĩa lý thuyết của các nhân tố được tạo ra: Đảm bảo rằng các nhân tố được hình thành không chỉ mang ý nghĩa thống kê mà còn phù hợp với cơ sở lý thuyết và mục tiêu nghiên cứu của bạn.

2.2 Kiểm định Bartlett (Bartlett’s test of sphericity)

Một giả định quan trọng trong EFA là các biến quan sát được đưa vào phân tích phải có sự tương quan với nhau. Thay vì đánh giá thông qua ma trận tương quan (vốn có thể phức tạp), chúng ta có thể sử dụng kiểm định Bartlett. Kiểm định này nhằm xác định liệu có mối tương quan giữa các biến tham gia vào EFA hay không, với giả thuyết: H₀: Không có sự tương quan giữa các biến quan sát.

Cách đánh giá:

• Nếu sig (p-value) < 0.05, ta bác bỏ H₀ và kết luận rằng các biến có tương quan với nhau, đáp ứng điều kiện để thực hiện EFA.
• Nếu sig ≥ 0.05, ta chấp nhận H₀, tức là các biến không có sự tương quan, và phân tích EFA không phù hợp trong trường hợp này.

Kiểm định Bartlett giúp đảm bảo tính hợp lý của việc áp dụng EFA vào bộ dữ liệu.

2.3 Xác định số nhân tố được trích

Theo Hair và cộng sự (2009), việc trích xuất nhân tố nên dựa trên sự kết hợp giữa cơ sở lý thuyết và kết quả thực nghiệm từ dữ liệu thu thập. Có nhiều phương pháp để xác định số lượng nhân tố tối ưu (hay điểm dừng trong phân tích EFA), bao gồm:

• Tiêu chí eigenvalue
• Tổng phương sai trích
• Biểu đồ Scree Plot
• Số nhân tố kỳ vọng dựa trên lý thuyết

Trong thực tế, các nhà nghiên cứu thường kết hợp nhiều phương pháp để đảm bảo độ tin cậy và tính chính xác của kết quả. Dưới đây là trình bày chi tiết về bốn phương pháp phổ biến này.

a. Tiêu chí Eigenvalue

Theo Hair và cộng sự (2009), chỉ những nhân tố có eigenvalue (hay còn gọi là latent roots) lớn hơn 1 mới được coi là có ý nghĩa thống kê và được giữ lại trong mô hình.

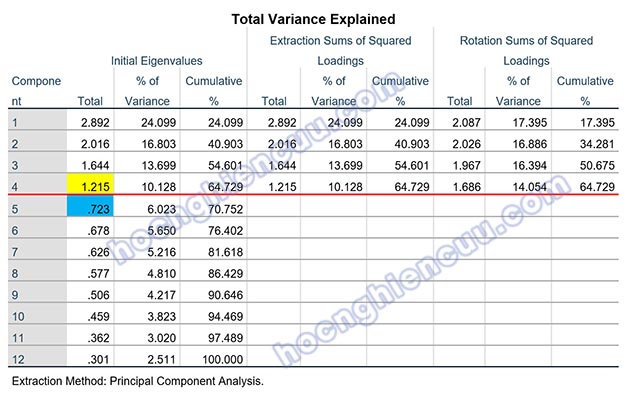
Bảng Total Variance Explained thường bao gồm các cột chính sau:

• Component: Liệt kê số nhân tố tiềm năng, bằng với số biến quan sát ban đầu.
• Initial Eigenvalues: Thể hiện giá trị eigenvalue ban đầu trước khi trích nhân tố. Mỗi nhân tố tương ứng với một giá trị eigenvalue.
• Extraction Sums of Squared Loadings: Thể hiện giá trị eigenvalue sau khi trích nhân tố. Ví dụ, từ 12 nhân tố ban đầu, quá trình trích có thể chỉ giữ lại 4 nhân tố đạt tiêu chuẩn.
• Rotation Sums of Squared Loadings: Thể hiện giá trị eigenvalue sau khi xoay nhân tố (nếu áp dụng phương pháp xoay).

Trong ví dụ minh họa, kết quả phân tích cho thấy:

• Nhân tố thứ 4 có eigenvalue = 1.215 (>1) → Đạt tiêu chuẩn, được giữ lại.
• Nhân tố thứ 5 có eigenvalue = 0.723 (<1) → Không đạt tiêu chuẩn, loại bỏ.

Kết luận: Theo tiêu chí eigenvalue ≥ 1, quá trình trích nhân tố sẽ dừng ở 4 nhân tố.

b. Tổng phương sai trích

Phương pháp này xác định số nhân tố cần trích dựa trên tỷ lệ phương sai tích lũy mà các nhân tố giải thích được cho tập biến quan sát. Có hai quan điểm chính về ngưỡng phương sai tối thiểu:

• Merenda (1997) đề xuất tổng phương sai tích lũy tối thiểu 50%
• Hair và cộng sự (2009) khuyến nghị ngưỡng 60% để đảm bảo chất lượng mô hình tốt hơn

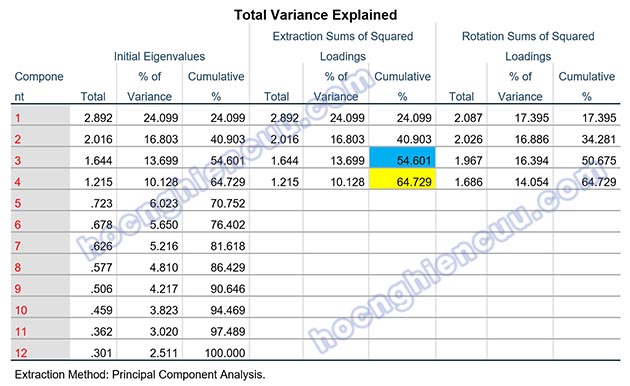
Trong bảng kết quả ở trên, từ nhân tố thứ ba trở đi, tổng phương sai trích được giải thích đạt mức trên 50%. Như vậy theo quan điểm của Merenda (1997) thì số nhân tố được trích nên từ 3 trở đi. Kết hợp với tiêu chí eigenvalue thì số nhân tố được trích tối ưu nên là 4 nhân tố tại phương sai tích lũy là 64.729% > 50%. Như vậy, 4 nhân tố được trích giải thích được (cô đọng được) 64.729% biến thiên dữ liệu của 12 biến quan sát tham gia vào EFA.

2.4 Hệ số tải nhân tố Factor Loading

Hệ số tải (còn gọi là trọng số nhân tố) thể hiện mức độ tương quan giữa biến quan sát và nhân tố. Trị tuyệt đối của hệ số tải càng cao, mối quan hệ giữa biến quan sát và nhân tố càng chặt chẽ, và ngược lại. Nếu trong cùng một nhân tố xuất hiện hệ số tải âm, điều đó cho thấy biến quan sát đó có xu hướng ngược chiều so với phần lớn các biến quan sát khác trong nhân tố. Khi đó, biến quan sát này có tương quan âm với các biến quan sát có hệ số tải dương trong cùng nhân tố.

Với cỡ mẫu tối thiểu là 100, Hair và cộng sự (2009) cho rằng:

• Trị tuyệt đối Factor Loading ở mức 0.3 đến 0.4: cân nhắc là điều kiện tối thiểu để biến quan sát được giữ lại.
• Trị tuyệt đối Factor Loading ở mức từ 0.5 trở lên: mức tối ưu, các biến quan sát có ý nghĩa thống kê tốt.

Tuy nhiên, Hair và cộng sự cho rằng việc xác định ngưỡng hệ số tải cũng cần xem xét đến cỡ mẫu. Nhóm tác giả đã đề xuất bảng tương ứng giữa cỡ mẫu và mức hệ số tải phù hợp, như sau:

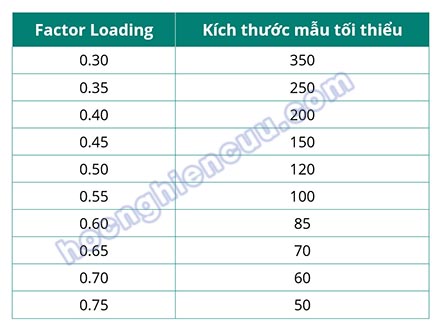
Các tác giả cho rằng bảng cỡ mẫu – hệ số tải tiêu chuẩn này mang tính tương đối và cần được xem xét cùng với số lượng biến quan sát cũng như số nhân tố trích được trong phân tích EFA để đánh giá chất lượng biến. Khi cỡ mẫu lớn hoặc số lượng biến trong EFA nhiều, có thể chọn ngưỡng hệ số tải thấp hơn. Ngược lại, nếu số nhân tố trích được nhiều, ngưỡng hệ số tải nên được đặt cao hơn để đảm bảo độ chính xác.

3. Phân tích nhân tố khám phá EFA trên SPSS 26

Tiến hành phân tích nhân tố khám phá EFA với một tập dữ liệu mẫu. Sau bước kiểm định Cronbach’s Alpha, biến LD7 không đạt độ tin cậy nên bị loại khỏi các bước phân tích tiếp theo. Chính vì vậy, ở bước đánh giá EFA (bước thực hiện sau Cronbach’s Alpha), chúng ta sẽ không đưa biến này vào phân tích. Với tính chất mô hình đơn giản, đã xác định rõ ràng biến độc lập, biến phụ thuộc. Chúng ta sẽ thực hiện phân tích nhân tố khám phá riêng cho biến độc lập và biến phụ thuộc.

Để thực hiện phân tích nhân tố khám phá trong SPSS 26, chúng ta vào Analyze > Dimension Reduction > Factor…

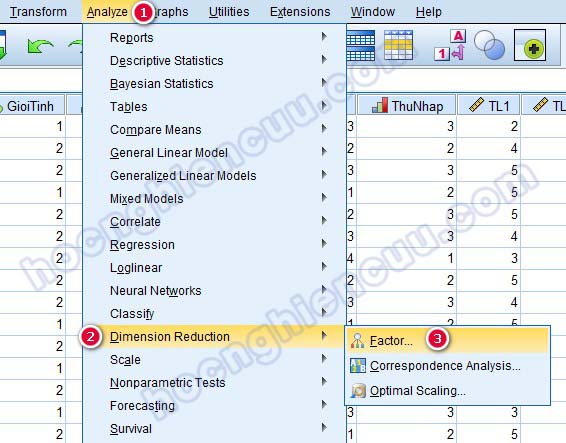
3.1 Phân tích EFA cho biến độc lập

Ngoại trừ biến LD7, đưa các biến quan sát độc lập còn lại vào mục Variables. Chú ý các tùy chọn bên phải, chúng ta sẽ đi qua lần lượt các tùy chọn này.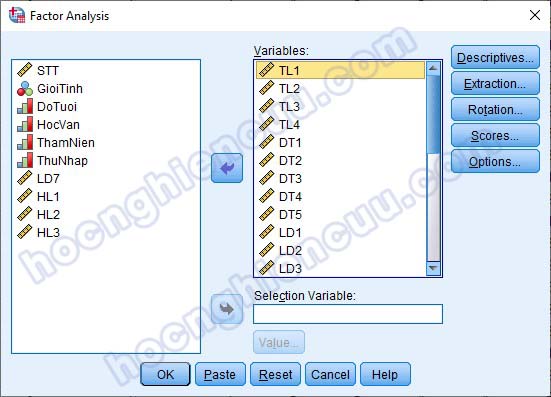

– Descriptives: Tích vào 3 mục: Initial solution, Coefficients, KMO and Barlett’s test of sphericity. Nhấp Continue để quay lại cửa sổ ban đầu.

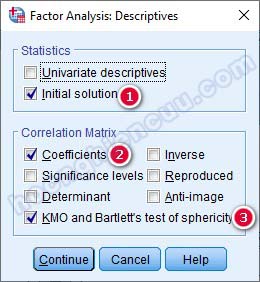
– Extraction: Đề tài nghiên cứu này là nghiên cứu lặp lại, đã có lý thuyết nền rõ ràng về các nhân tố, thang đo. Chúng ta sẽ sử dụng phép trích PCA (Principal Components hoặc Principal Components Analysis) với mục đích thu gọn số lượng biến quan sát về các nhân tố tóm tắt thông tin tốt nhất và tiêu chí trích Eigenvalue lớn hơn 1. Tích chọn vào các mục Scree Plot, Based on Eigenvalue.

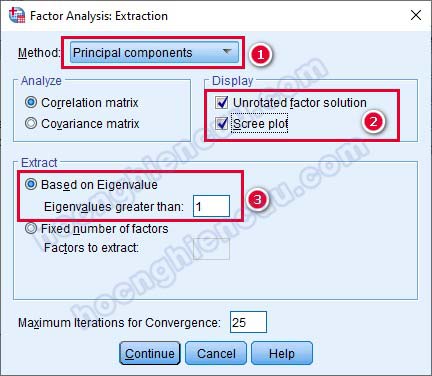
– Rotation: Mô hình nghiên cứu chỉ có biến độc lập và biến phụ thuộc, do vậy phép quay Varimax là phù hợp nhất. Nhấp Continue để quay lại cửa sổ ban đầu.

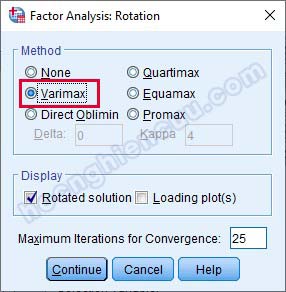
– Options: Tích vào Sorted by size để ma trận xoay sắp xếp thành từng cột dạng bậc thang để dễ đọc kết quả hơn, chúng ta có thể tích hoặc không tích, việc này không ảnh hưởng đến kết quả. Cần nhớ rằng, thứ tự các nhân tố trong kết quả ma trận xoay không phản ánh mức độ quan trọng của nhân tố đó. Với mục Suppress small coefficients, nếu không tích chọn, ma trận xoay sẽ hiển thị toàn bộ hệ số tải của mỗi biến quan sát ở từng nhân tố.

Trường hợp chỉ muốn ma trận xoay hiện lên những ô có hệ số tải từ 0.3, 0.4 hay 0.5 … trở lên, chúng ta sẽ tích vào Suppress small coefficients. Lúc này hàng Absolute value below sẽ sáng lên và cho phép nhập vào ngưỡng hệ số tải mà nếu hệ số tải dưới ngưỡng đó sẽ không hiển thị trong bảng ma trận xoay. Trong ví dụ thực hành này, để tiện cho việc theo dõi kết quả, tác giả muốn ma trận xoay chỉ hiển thị các ô có hệ số tải từ 0.3 trở lên nên sẽ nhập vào 0.3. Sau đó nhấp vào Continue để đóng cửa sổ.

Tại cửa sổ tiếp theo, chọn OK để xuất kết quả ra output.

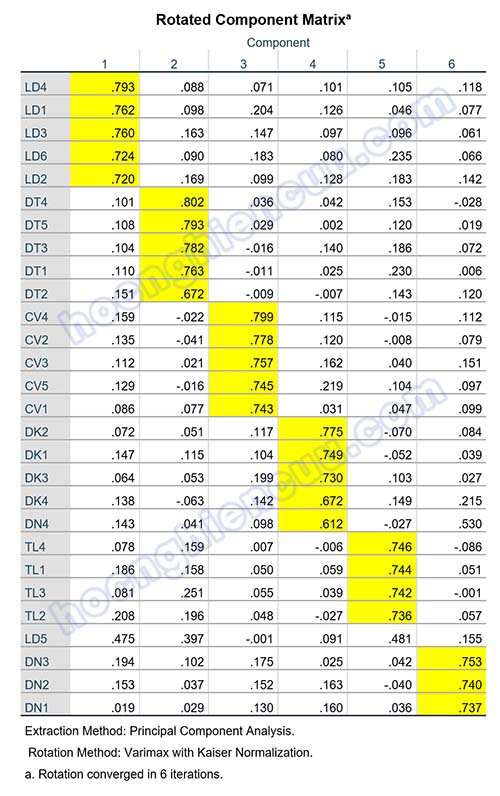
Có khá nhiều bảng ở output, tất cả các bảng này đều đóng góp vào việc đánh giá kết quả phân tích EFA là tốt hay tệ. Tuy nhiên, ở đây tác giả tập trung vào ba bảng kết quả chính: KMO and Barlett’s Test, Total Variance Explained và Rotated Component Matrix, bởi sử dụng ba bảng này chúng ta đã có thể đánh giá được kết quả phân tích EFA phù hợp hay không phù hợp.

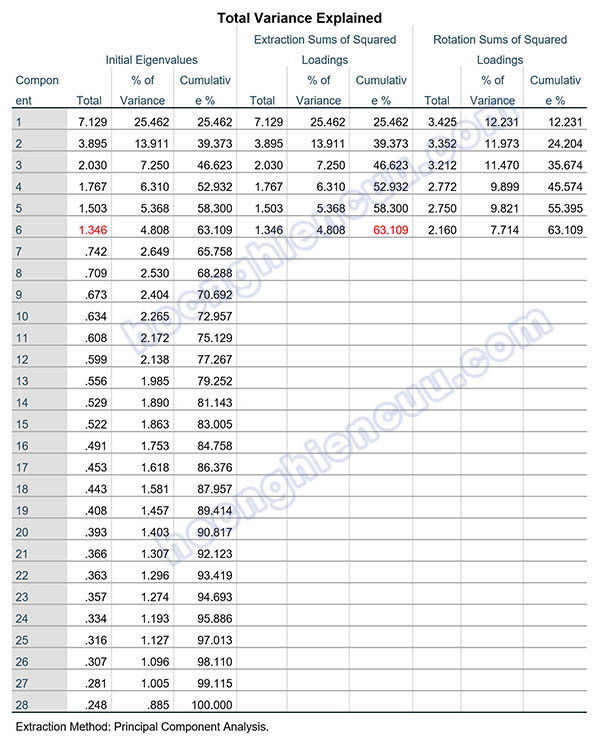
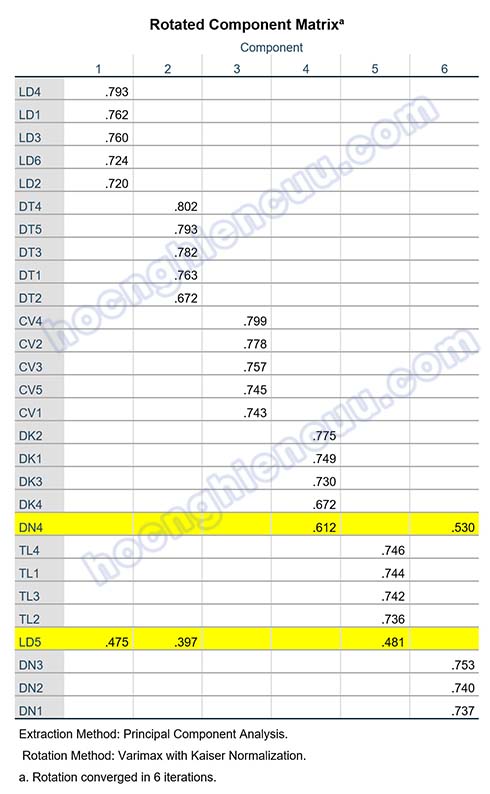
Kết quả lần EFA đầu tiên: KMO = 0.887 > 0.5, sig Bartlett’s Test = 0.000 < 0.05, như vậy phân tích nhân tố khám phá EFA là phù hợp. Có 6 nhân tố được trích với tiêu chí eigenvalue lớn hơn 1 với tổng phương sai tích lũy là 63.109%. Tác giả mong muốn chọn ra các biến quan sát chất lượng nên sẽ sử dụng ngưỡng hệ số tải là 0.5 thay vì chọn hệ số tải tương ứng theo cỡ mẫu. So sánh ngưỡng này với kết quả ở ma trận xoay, có hai biến xấu là DN4 và LD5 cần xem xét loại bỏ:

• Biến DN4 tải lên ở cả hai nhân tố là Component 4 và Component 6 với hệ số tải lần lượt là 0.612 và 0.530, mức chênh lệch hệ số tải bằng 0.612 – 0.530 = 0.082 < 0.2.
• Biến LD5 có hệ số tải ở tất cả các nhân tố đều nhỏ5.

Tác giả sử dụng phương thức loại một lượt các biến xấu trong một lần phân tích EFA. Từ 28 biến quan sát ở lần phân tích EFA thứ nhất, loại bỏ DN4 và LD5 và đưa 26 biến quan sát còn lại vào phân tích EFA lần thứ hai.

Hệ số KMO = 0.879 > 0.5, sig Barlett’s Test = 0.000 < 0.05, như vậy phân tích nhân tố là phù hợp.

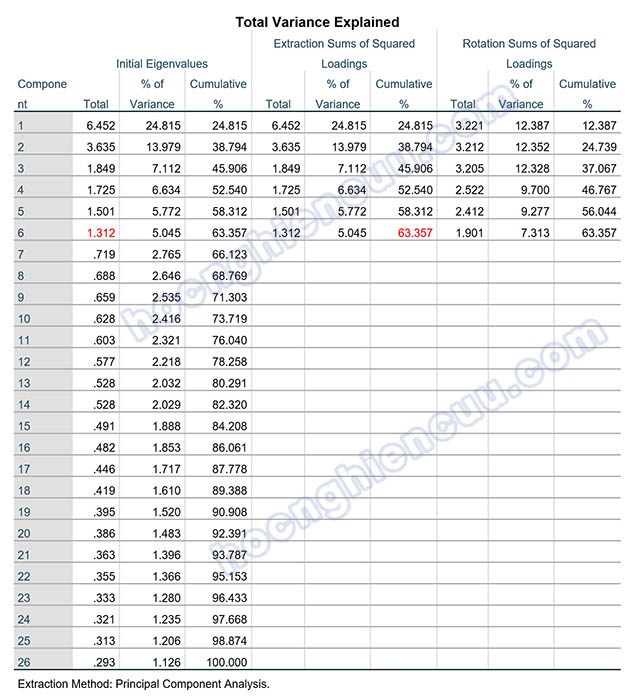
Có 6 nhân tố được trích dựa vào tiêu chí eigenvalue lớn hơn 1, như vậy 6 nhân tố này tóm tắt thông tin của 26 biến quan sát đưa vào EFA một cách tốt nhất. Tổng phương sai mà 6 nhân tố này trích được là 63.357% > 50%, như vậy, 6 nhân tố được trích giải thích được 63.357% biến thiên dữ liệu của 26 biến quan sát tham gia vào EFA.

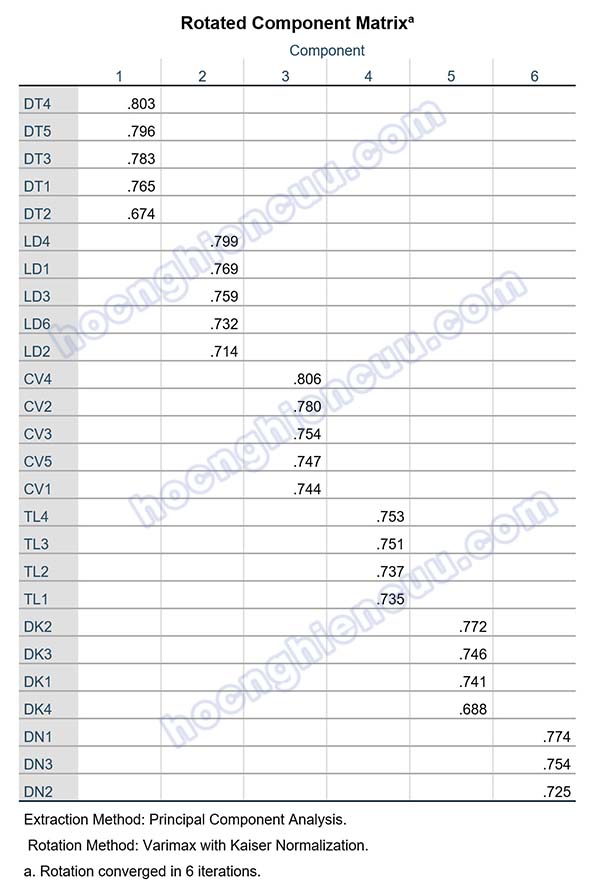
Kết quả ma trận xoay cho thấy, 26 biến quan sát được phân thành 6 nhân tố, tất cả các biến quan sát đều có hệ số tải nhân tố Factor Loading lớn hơn 0.5 và không còn các biến xấu.

Như vậy, phân tích nhân tố khám phá EFA cho các biến độc lập được thực hiện hai lần. Lần thứ nhất, 28 biến quan sát được đưa vào phân tích, có 2 biến quan sát không đạt điều kiện là DN4 và LD5 được loại bỏ để thực hiện phân tích lại. Lần phân tích thứ hai (lần cuối cùng), 26 biến quan sát hội tụ và phân biệt thành 6 nhân tố gồm các biến quan sát được trình bày trong bảng bên dưới:

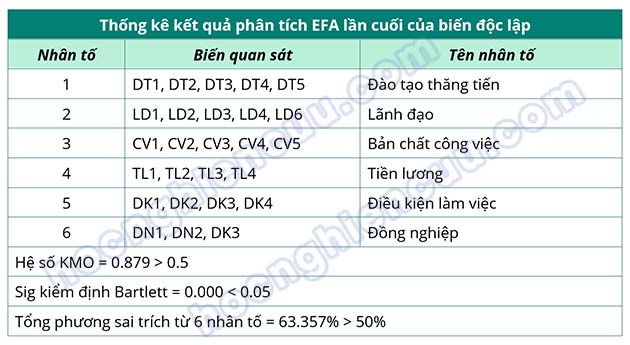
Nếu bạn đang gặp khó khăn trong phân tích nhân tố khám EFA trên SPSS như quá nhiều biến quan sát bị loại, cấu trúc nhân tố bị phá vỡ so với lý thuyết, ma trận xoay không đảm bảo được tính hội tụ – phân biệt,… Bạn có thể tham khảo qua dịch vụ SPSS của DVS để bên mình có thể tư vấn và hỗ trợ bạn xử lý các vấn đề của bài nhé.

3.2 Phân tích EFA cho biến phụ thuộc

Tương tự với các thao tác trên biến độc lập, tiến hành thực hiện phân tích nhân tố khám phá EFA cho biến phụ thuộc.

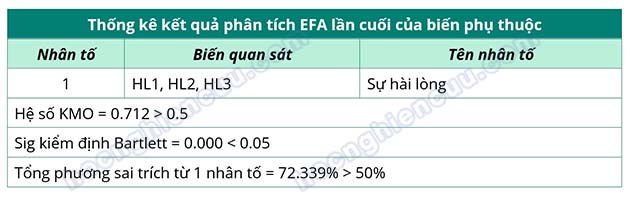
Hệ số KMO = 0.712 > 0.5, sig Barlett’s Test = 0.000 < 0.05, như vậy phân tích nhân tố là phù hợp.

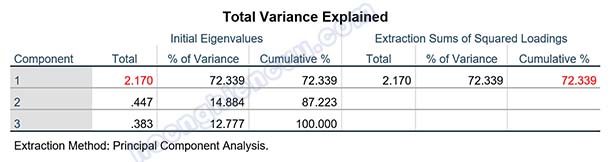
Kết quả phân tích cho thấy có 1 nhân tố được trích tại eigenvalue bằng 2.170 > 1. Nhân tố này giải thích được 72.339% biến thiên dữ liệu của 3 biến quan sát tham gia vào EFA.

Như đã đề cập trước đó ở mục 9.7. Nếu chỉ có một nhân tố được trích, ma trận xoay sẽ không hiển thị, chính vì vậy chúng ta sẽ đánh giá kết quả qua bảng ma trận nhân tố chưa xoay. Kết quả cho thấy 3 biến quan sát hội tụ về 1 cột và tất cả các biến quan sát đều có hệ số tải nhân tố lớn hơn 0.5.

Lưu ý rằng, nếu sau bước phân tích nhân tố EFA, cấu trúc thang đo bị thay đổi so với thang đo gốc: hình thành nhân tố mới, nhân tố giảm biến quan sát, nhân tố tăng biến quan sát… Chúng ta nên thực hiện kiểm định độ tin cậy thang đo Cronbach’s Alpha để đánh giá lại các thang đo mới được hình thành sau EFA.