Bài viết này sẽ tiếp nối nội dung bài Xử lý mô hình biến bậc hai, biến bậc cao trong SMARTPLS. Do vậy, bạn cần xem toàn bộ nội dung bài viết trên để nắm được phần lý thuyết mở đầu mới có thể hiểu được nội dung sắp đề cập dưới đây.
Cách đọc kết quả ở mô hình bậc cao mà mối quan hệ biến bậc hai – biến bậc một ở dạng nguyên nhân hay kết quả sẽ khác nhau cực kỳ nhiều. Do vậy, các bạn cần phải xác định chính xác dạng thang đo của biến bậc hai với biến bậc một. Bài viết này sẽ hướng dẫn các bạn chi tiết cách đánh giá mô hình SEM bậc hai trên SMARTPLS mà mối quan hệ biến bậc hai – biến bậc một ở dạng kết quả (reflective).
Ở bài viết Xử lý mô hình biến bậc hai, biến bậc cao trong SMARTPLS chúng ta đã làm quen với biến HOC Chất lượng dịch vụ dạng nguyên nhân. Trong bài viết này, chúng ta giả định rằng mối quan hệ của biến Chất lượng dịch vụ với bốn biến bậc một: Nhân viên (4 biến quan sát), Giá cả (3 biến quan sát), Cơ sở vật chất (4 biến quan sát) là dạng kết quả. Toàn bộ các LOC cũng đều ở dạng kết quả.
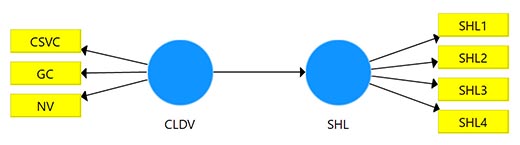
Khi biểu diễn lên diagram, chúng ta sẽ nối mũi tên hướng từ HOC (CLDV) lên các LOC (NV, GC, CSV) như sau:
Thực hiện đánh giá mô hình đo lường các LOC, lấy kết quả trọng số nhân tố các LOC hoàn toàn tương tự như mô hình bậc hai dạng kết quả, xem bước 2, bước 3 ở bài viết Xử lý mô hình biến bậc hai, biến bậc cao trong SMARTPLS.
Bước 4: Tạo diagram mới cho giai đoạn hai của kỹ thuật hai giai đoạn.
Tiến hành tạo một diagram mới biểu diễn các biến LOC vào mô hình. Lúc này từ mô hình bậc hai chúng ta đã chuyển về mô hình bậc một cơ bản. Biến tiềm ẩn CLDV từ bậc hai chuyển thành biến tiềm ẩn bậc một, các LOC gồm CSVC, GC, NV chuyển thành biến quan sát.
Các bước phía sau trở đi, chúng ta sẽ chỉ làm việc với diagram mới này.
Bước 5: Đánh giá mô hình đo lường HOC dạng kết quả
Mô hình của HOC là dạng kết quả (mối quan hệ biến bậc hai – biến bậc một ở dạng kết quả), chúng ta dựa theo cách đọc kết quả ở bài viết Đánh giá mô hình đo lường dạng kết quả trên SMARTPLS nhưng có một số điều chỉnh như bên dưới:
1. Đánh giá chất lượng biến bậc một
Thực hiện phân tích PLS Algorithm để đánh giá chất lượng biến bậc một. Từ output, nhấp vào Outer Loadings.
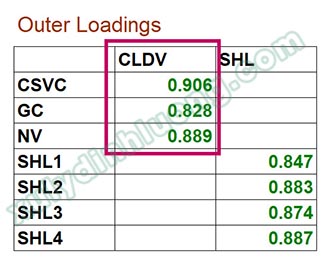
Chúng ta sẽ đánh giá Outer Loadings của các biến bậc một hoàn toàn tương tự như các biến quan sát ở dạng kết quả.
→ Hệ số Outer Loadings của các biến bậc một đều lớn hơn 0.7, như vậy các biến bậc một đều có ý nghĩa trong mô hình (Hair và cộng sự, 2016).
2. Đánh giá độ tin cậy, tính hội tụ, tính phân biệt
Sẽ không đánh giá các yếu tố này cho mô hình HOC. Hoặc chúng ta sẽ đánh giá độ tin cậy và tính hội tụ, không cần đánh giá tính phân biệt (do đã đánh giá tính phân biệt cho LOC ở giai đoạn một rồi, việc đánh giá tính phân biệt cho HOC không còn mang ý nghĩa).
→ Biến bậc hai CLDV có độ tin cậy, độ hội tụ cao khi các chỉ số Cronbach Alpha, CR đều lớn hơn 0.7 và AVE lớn hơn 0.5.
Bước 6: Đánh giá mô hình cấu trúc có biến bậc hai.
1. Đánh giá cộng tuyến giữa các biến trong mô hình
Chúng ta vẫn đánh giá cộng tuyến giữa các biến trong mô hình một cách bình thường dựa vào bảng Inner VIF Values từ phân tích PLS Algorithm ở giai đoạn hai.
→ Do trong hình huống này chỉ có một mối tác động từ CLDV lên SHL nên VIF luôn luôn bằng 1. Trường hợp có nhiều mối tác động hơn sẽ có nhiều giá trị VIF hơn. Nếu tất cả Inner VIF Values trong bảng này dưới ngưỡng 5 (hoặc 3, tùy ngưỡng sử dụng) thì mô hình không xảy ra tình trạng cộng tuyến.
2. Đánh giá các mối tác động
→ Biến CLDV có tác động lên SHL do P Values kiểm định t bằng 0.000 < 0.05. Nếu có nhiều biến tác động vào SHL, chúng ta sẽ dùng hệ số tác động chuẩn hóa Original Sample để so sánh sự tác động mạnh yếu giữa giữa các biến độc lập.
4. Mức độ giải thích của biến độc lập cho phụ thuộc (R bình phương)
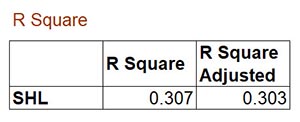
Để đánh giá hệ số R bình phương, chúng ta sẽ sử dụng kết quả R Square của phân tích PLS Algorithm.
→ R bình phương hiệu chỉnh của SHL bằng 0.303, như vậy biến độc lập CLDV giải thích được 30.3% sự biến thiên (phương sai) của biến SHL.
5. Mức độ ảnh hưởng của biến độc lập effect size f2 (f bình phương)
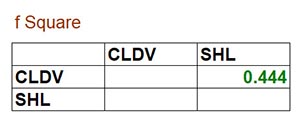
Để đánh giá hệ số f2 (f bình phương), chúng ta sẽ sử dụng kết quả f Square của phân tích PLS Algorithm.
Cohen (1988) đã đề xuất bảng chỉ số f Square để đánh giá tầm quan trọng của các biến độc lập như sau:
- f Square < 0.02: mức tác động là cực kỳ nhỏ hoặc không có tác động.
- 0.02 ≤ f Square < 0.15: mức tác động nhỏ.
- 0.15 ≤ f Square < 0.35: mức tác động trung bình.
- f Square ≥ 0.35: mức tác động lớn.
→ Giá trị f Square của CLDV bằng 0.444, do vậy, CLDV tác động lên SHL ở mức mạnh.