Một trong các giả định khi thực hiện hồi quy tuyến tính đa biến là giả định phương sai không đổi (hay còn gọi là phương sai đồng nhất). Nếu xảy ra hiện tượng phương sai thay đổi, kết quả của phương trình hồi quy sẽ không chính xác, làm sai lệch kết quả so với thực tế, từ đó khiến người nghiên cứu đánh giá nhầm chất lượng của phương trình hồi quy tuyến tính.
1. Lý thuyết về giả định phương sai không đổi trong hồi quy tuyến tính
Để đánh giá mô hình hồi quy có vi phạm giả định này hay không, chúng ta sẽ dựa vào biểu đồ Scatter Plot giữa các phần dư chuẩn hóa và giá trị dự đoán chuẩn hóa của phép hồi quy. Nếu các điểm dữ liệu tạo thành dạng đám mây có độ lớn trải đều nhau dọc theo đường tung độ 0, chúng ta có thể kết luận giả định phương sai không đổi không bị vi phạm (thường vùng phân tán của các điểm dữ liệu trên trục tung nằm trong đoạn -3 đến 3 là tốt).
Bên cạnh việc đánh giá hiện tượng phương sai không đổi qua đồ thị scatter, chúng ta có thể sử dụng các kiểm định như White, Glesjer, tương quan hạng Spearman để đánh giá chính xác hơn giả định này. Các kiểm định White và Glesjer hiện tại vẫn chưa hỗ trợ sẵn trên phiên bản SPSS 26 mới nhất, để thực hiện các kiểm định này phải trải qua các thao tác trung gian khá nhiều và phức tạp. Do vậy, việc sử dụng tương quan hạng Spearman để đánh giá mối quan hệ giữa phần dư và các biến độc lập sẽ là phương thức thuận tiện hơn rất nhiều để xem xét hiện tượng phương sai không đổi bằng SPSS.
Nếu giá trị sig tương quan Spearman giữa phần dư chuẩn hóa (ABSZRE) với các biến độc lập đều lớn hơn 0.05, ta có thể kết luận rằng không có hiện tượng phương sai thay đổi xảy ra. Trường hợp có ít nhất một giá trị sig nhỏ hơn 0.05, khi đó mô hình hồi quy đã vi phạm giả định phương sai không đổi, chúng ta sẽ cân nhắc loại các biến độc lập có giá trị sig tương quan Spearman với ABSZRE lớn hơn 0.05 và phân tích lại hồi quy.
2. Đánh giá giả định phương sai không đổi trên SPSS 26
Ví dụ bên dưới là một phép hồi quy với biến phụ thuộc F_HL và sáu biến độc lập F_LD, F_DN, F_CV, F_TL, F_DT, F_DK.
a. Đánh giá giả định phương sai không đổi dựa vào đồ thị Scatter
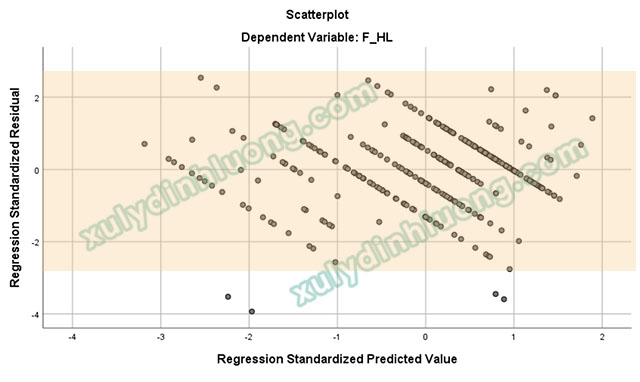
Kết quả phân tích hồi quy tuyến tính cho đồ thị Scatter như sau:
Theo Pituch & Stevens (2016), các điểm dữ liệu phần dư trong đồ thị scatter dao động chủ yếu trong đoạn -3 đến 3 được xem như là điều kiện tốt xác nhận không xảy ra phương sai thay đổi. Từ kết quả đồ thị Scatter Plot bên trên có thể thấy các điểm dữ liệu phần dư tạo thành dạng đám mây có độ lớn trải đều nhau dọc theo đường tung độ 0 và dao động trong vùng -3 đến 3, như vậy giả định phương sai không đổi không bị vi phạm.
b. Đánh giá giả định phương sai không đổi dựa vào tương quan hạng Spearman
Bên cạnh việc kiểm tra giả định phương sai không đổi bằng đồ thị Scatter Plot của phần dư chuẩn hóa, chúng ta có thể sử dụng tương quan hạng Spearman đánh giá mối quan hệ giữa phần dư và các biến độc lập. Thực hiện phân tích lại hồi quy tuyến tính bội, các tùy chọn chúng ta vẫn giữ như cũ, nhấp chuột vào mục Save.
Cửa sổ Save hiện ra, tích vào ô Standardized như hình bên dưới để xuất dữ liệu phần dư chuẩn hóa, phục vụ cho việc kiểm tra vi phạm giả định phương sai không đổi. Sau đó chọn Continue, OK để xuất kết quả ra output.
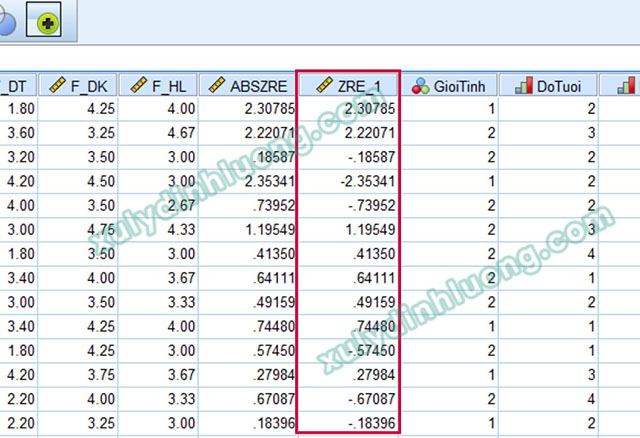
Quay lại giao diện Data View, chúng ta sẽ thấy xuất hiện thêm một biến mới có tên là ZRE_1 chính là phần dư chuẩn hóa của kết quả hồi quy.
Chúng ta không làm việc trực tiếp với biến ZRE_1 mà sẽ lấy trị tuyệt đối của biến này. Vào Transform > Compute Variable…
Trong mục Target Variable, đặt tên cho biến trị tuyệt đối của ZRE_1. Chúng ta có thể đặt tên tùy ý, trong trường hợp này tác giả lấy tên ABSZRE (ABS: hàm trị tuyệt đối; ZRE: phần dư chuẩn hóa). Mục Numeric Expression, nhập hàm ABS(ZRE_1), nhấp vào OK.
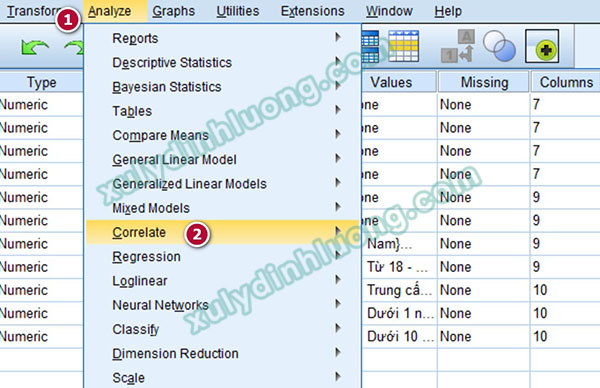
Thực hiện phân tích tương quan hạng Spearman, vào Analyze > Correlate > Bivariate…
Đưa biến ABSZRE và các biến độc lập vào mục Variables. Tích chọn vào mục Spearman như hình bên dưới (nên đưa biến ABSZRE lên trên cùng), sau đó nhấp OK.
Output sẽ xuất ra kết quả tương quan hạng, chúng ta chú ý tới hàng giá trị sig mối tương quan giữa ABSZRE với các biến độc lập.
Tất cả giá trị sig mối tương quan hạng giữa ABSZRE với các biến độc lập đều lớn hơn 0.05, do đó phương sai phần dư là đồng nhất, giả định phương sai không đổi không bị vi phạm.